Quite often, an engineer is confronted with the task of analyzing dynamic or transient type processes. These processes are generally modeled by using ordinary differential equations or partial differential equations. These differential equations can be highly nonlinear in nature, and analytical solutions are either very difficult or even impossible to achieve. As a result, numerical techniques must often be employed to integrate these systems.
In our previous paper (1) in this series of two papers, we employed a BASIC algorithm to perform the necessary integrations for several dynamic or transient-type processes. These illustrations considered only open-loop type problems. For instance, if the concentration of a reactant species in the feed stream to a CSTR reactor was perturbed, we proceeded to model and observe the time-varying response of the remaining reactant concentration in the effluent stream.
In this second paper of the series, we extend the application of the BASIC algorithmic scheme to closed-loop process control systems employing negative feedback. The first page of the paper describes a typical process control scenario for a simple liquid level-flow system. A brief review of the various general type ideal controller schemes is presented first followed by a review of the basis for the algorithmic structure. Then we present three specific illustrations which simulate process control for the following dynamic processes:
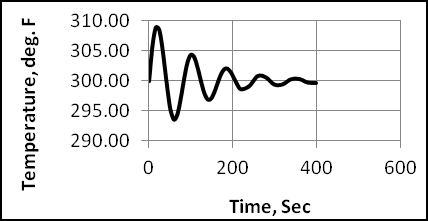
- A heated tank with inflow and outflow of liquid where it is desired to control the temperature of the outflow stream.
- Two interacting tanks involving a liquid level-flow network where we wish to control the liquid level in the second tank.
- Two CSTR reactors operating in series where it is required that we control the concentration of the remaining reactant in the effluent from the second reactor.
